chapter 1 AVL Tree、Splay Tree and Amortized Analysis¶

AVL Tree(speed up searching)¶

Info

An empty binary tree is height balanced. If \(T\) is a nonempty binary tree with \(T_L\) and \(T_R\) as its left and right subtrees, then \(T\) is height balanced iff (1) \(T_L\) and \(T_R\) are height balanced, and (2) \(| h_L - h_R | \leq 1\) where \(h_L\) and \(h_R\) are the heights of \(T_L\) and \(T_R\) , respectively.

这里定义Balance Factor(BF) = \(h_L - h_R\)来判断树的平衡性，在一个AVL Tree中，\(BF = -1, 0, 1\)

Warning

对于空节点，其BF默认为-1
对于单节点，其BF默认为0

Tree Rotation¶

Warning

通过Rotation处理非平衡的情况依照从叶子节点向上，先解决最低的

Right(or Left)Rotation¶

Tree rotation is an operation on a binary tree that changes the structure without interfering with the order of the elements.

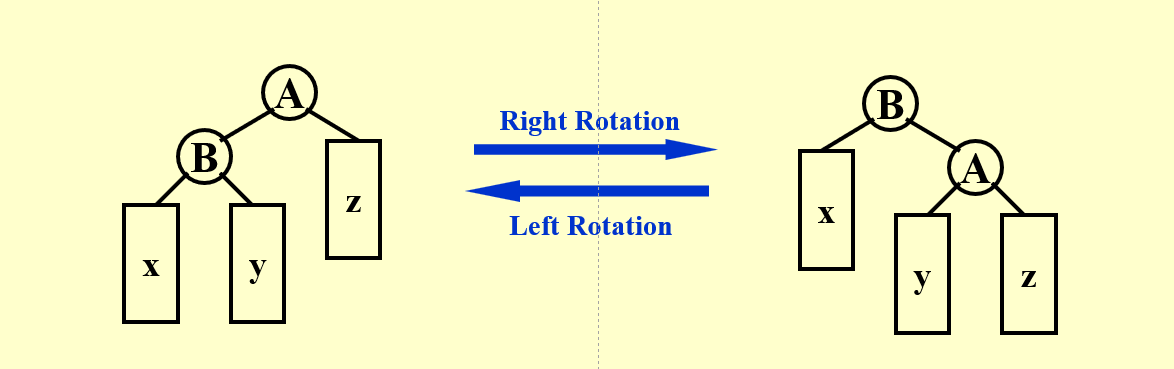
After a rotation, the side of the rotation increases its height by 1 whilst the side opposite the rotation decreases its height similarly.
Time complexity: \(O(1)\)

Example

The trouble maker Nov is in the right subtree’s right subtree of the trouble finder Mar. Hence it is called an RR rotation.

Double Rotation¶

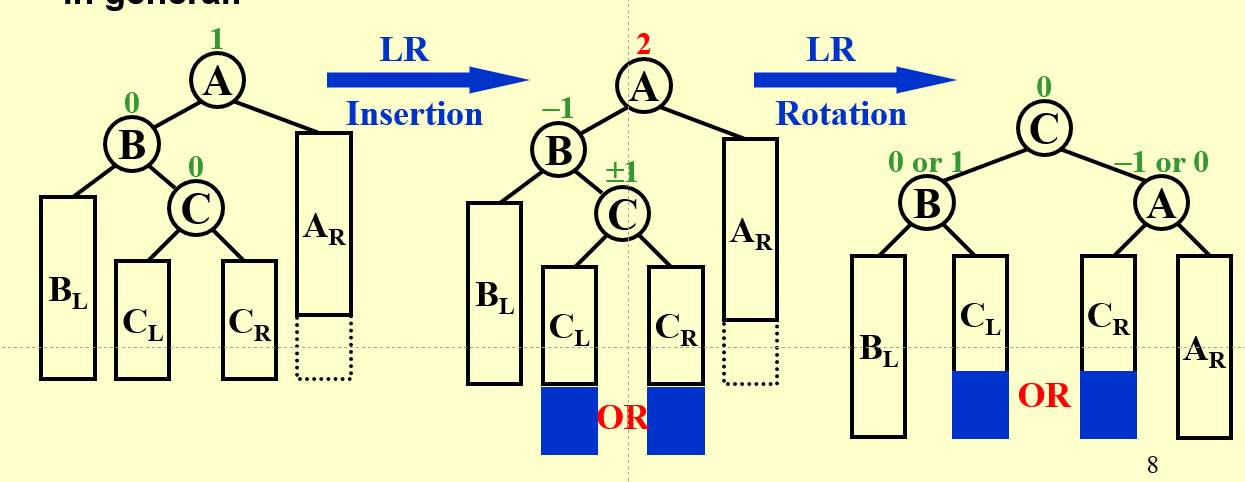
Minimum Number of Nodes¶

Let \(n_h\) be the minimum number of nodes in a height balanced tree of height \(h\). Then the tree must look like

\(F_0 = 0, F_1 = 1, F_i = F_{i-1} + F_{i-2}\) \(for\) \(i > 1\)

\(n_h = F_{h+3} - 1, for \quad h \leq -1\)

Splay Tree¶

Abstract

Target: Any \(M\) consecutive tree operations starting from an empty tree take at most \(O(M log N)\) time.
Idea: After a node is accessed, it is pushed to the root by a series of AVL tree rotations

为了避免出现冗余的循环后回到原点，对Splay Tree的处理采用zig-zig和zig-zag两种方式。

Tip

Splay 树的想法一方面来源于希望可以不像 AVL 那样保持严格的平衡约束，但也能保证某种层面（均摊）的对数时间复杂度，另一方面 Splay 树在访问（特别注意访问包括搜索、插入和删除）时都需要将元素移动到根结点，这非常符合程序局部性的要求，即刚刚访问的数据很有可能再次被访问，因此在实现缓存和垃圾收集算法中有一定的应用。

搜索：使用普通二叉搜索树的方法找到结点，然后通过 splay 操作经过一系列旋转将搜索的结点移动到根结点的位置
插入：使用普通二叉搜索树的方法找到要插入的位置进行插入，然后把刚刚插入的结点通过splay操作经过一系列旋转移动到根结点的位置
删除：使用普通二叉搜索树的方法找到要删除的结点，然后通过 splay 操作经过一系列旋转将要删除的结点移动到根结点的位置，然后删除根结点（现在根结点就是要删除的点），然后和普通二叉搜索树的删除一样进行合理的merge即可。

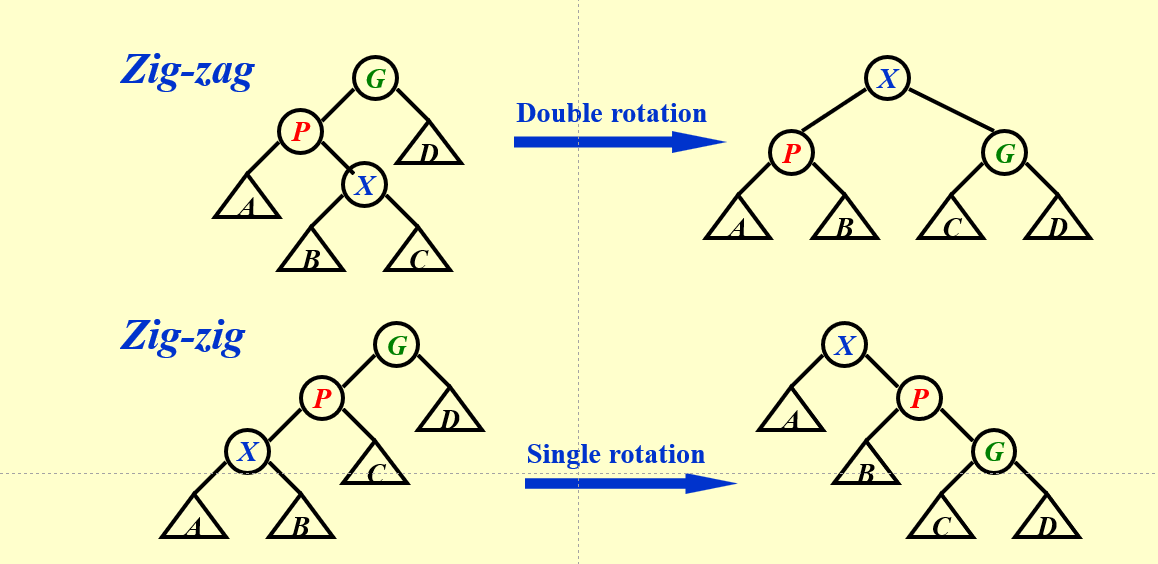
Zig-zig

zig-zig虽然写作single rotation，但是其实际上旋转了两次，先是G与P交换位置(G变为P的右子树)，再交换P与X的关系(P变为X的右子树)

Amortized Analysis(摊还分析)¶

Abstract

摊还分析的想法来源于我们希望估计一种数据结构经过一系列操作的平均花费时间。然而，平均时间非常难计算，因为每一步都有非常多的选择，连续m个操作，可能的操作路径是指数级别的。并且有时候平均涉及概率分布等，但我们并不知道确切的分布，因此比较难以计算。一种最简单的估计方法就是用最差情况分析作为平均情况的上界，例如Splay树，每个操作最差都是\(O(n)\)（\(n\)为树中结点个数）的，因此平均不会比最差情况差，所以也是\(O(n)\)的。然而这样的估计显然是放得太宽了，我们对这个复杂度是非常不满意的，因此我们需要进行摊还分析。事实上，在最差情况的分析中，我们忽略了一件事情，就是有的序列是不可能出现的，例如直接在空的树上用\(O(n)\)时间删除，摊还分析则是希望排除掉最差情况分析中把所有不管可能不可能的情况，最差的路径挑出来的这种无脑行为，转而分析所有可能的从空结构开始的操作路径中，最差的平均时间，那么这一时间一定比最差情况分析好，因为排除掉了一些不可能出现的所谓最差序列，但又会大于等于平均时间，因为取的是所有可能序列中最差的那一种。因此当我们算出摊还分析的时间复杂度，那么它也一定是平均时间的上界，同时这个上界会比最差情况分析好，这也是不等式worst-case bound \(≥\) amortized bound \(≥\) average-case bound的内在含义。

接下来我们介绍三种方法：聚合分析、核算法以及势能法。聚合分析直接使用了我们上面提到的思想：“摊还分析是考虑可能出现的操作序列中的最差序列”（再次强调，这里的最差不是最差情况分析的最差，最差情况分析的最差会包括不可能出现的序列，但摊还分析要排除不可能的序列）

Aggregate analysis(聚合分析)¶

Example

思考这一支持 MultiPop 操作的栈，在从空栈开始的连续 n 次操作中，最差的情况是什么：实际上就是先 Push n−1个然后最后一次操作一次性 Multipop 出所有元素。为什么这样是最差的呢？事实上简单想想就能理解，无法理解或者希望严谨一些可以看下面的解释：因为 n 次操作是固定的，所以我们的目标是，固定 n 的情况使得下总的代价最大，普通的 Push 和 Pop 都是 1 次操作对应1 个单位代价，所以我们必须寄希望于序列中 MultiPop 代价最大，那代价最大的情况就是只 MultiPop一次，且就在最后一次，因为如果只 MultiPop 一次，不在最后一次，显然这次 MultiPop 代价比 n − 1小；如果 MultiPop 多次，那么 Push 操作的个数少了，所以 MultiPop 能弹出的比 n − 1 少，所以代价也少。

Accounting method(核算法)¶

核算法就是传统意义上的取长补短

\[\sum\limits_{i=1}^{n}\hat{c_i} \geq \sum\limits_{i=1}^{n}{c_i}\]

\(\hat{c_i}\)是预测的期望(摊还代价)，\(c_i\)是实际的开销，他们满足\(\hat{c_i} = c_i + \Delta_i\)，\(\Delta_i\)是截取的长或者是补足的短。(可正可负)

一个悲伤的例子

当然你也可以说，你希望你的平均绩点保持在4.0以上，你知道ADS这门课你可能会挂科，所以你之前的微积分、线性代数、FDS等就需要为这次挂科存下足够高的均绩。

Potential method(势能法)¶

势函数

比如思考 Splay 树这种复杂的结构，所以我们希望有一个更统一的方法解决这个问题：我们不再把目光局限于每个操作，而是给整个结构定义一个势函数，这个势函数描述了这个结构不同状态，其实就是借用了物理里面的势能的思想，比如重力势能是高度的函数，但树的势能可能是树高的函数，也可能是树的结点总数的函数甚至更复杂等等。

\[ \sum\limits_{i=1}^{n}\hat{c_i} = \sum\limits_{i=1}^{n}({c_i}+\Phi(D_i)-\Phi(D_{i-1})) = \sum\limits_{i=1}^{n}{c_i} + \Phi(D_n) - \Phi(D_0) \]

Attention

注意这里的\(i\)不再是核算法中表示第\(i\)种操作，而是\(n\)个操作组成的序列中的第\(i\)个！因此这里的含义是，每一步的摊还代价等于真实操作的代价加上势函数的变化

如何设计势函数

为了使得摊还成本是平均成本的上界，我们仍然需要满足\(\sum\limits_{i=1}^{n}\hat{c_i} \geq \sum\limits_{i=1}^{n}{c_i}\)因此只需要满足\(\Phi(D_n) \leq \Phi(D_0)\)即可，这一点在设计函数的时候很容易满足，因为我们可以通过调整使得 \(Φ(D_0) = 0\)，即初始状态势能为0，其它任何状态的势能都不会小于0就可以了，这比考虑核算法中对任何可能的序列都成立更加简单直接，因此更多时候我们采用势能法进行分析。

Splay树的摊还分析¶

Rank of SubTree

节点数目的对数，为什么不用Height,Height不能很好的反应数量，且不会严格增加

\[ \sum\limits_{i=1}^{n}\hat{c_i} \leq 1 + 3(R_{k+1}(X)-R_{k}(X)) + \sum\limits_{i=1}^{k}3(R_i(X)-R_{i-1}(X)) = 1 + 3(R_{k+1}(X) - R_0(X)) = O(logN) \]

算法导论上的例子¶

栈操作¶

例子描述

PUSH(S, x) : 将对象x压入栈S中
POP(S) : 将栈S的栈顶对象弹出，并返回该对象，对空栈调用POP会产生一个错误
MULTIPOP(S, k) : 将栈S的k个栈顶对象弹出

聚合分析

通过使用聚合分析，我们考虑整个序列的\(n\)个操作，可以得到更好的上界。实际上，虽然一个单独的 MULTIPOP操作可能代价很高，但在一个空栈上执行\(n\)个 PUSH、 POP和MULTIPOP的操作序列，代价至多是 \(O(n)\)。这是为什么呢？当将一个对象压入栈后，我们至多将其弹出一次。因此，对一个非空的栈，可以执行的 POP操作的次数（包括了MULTIPOP中调用POP的次数）最多与PUSH操作的次数相当，即最多\(n\)次。因此，对任意的 n值，任意一个由\(n\)个 PUSH、 POP和 MULTIPOP组成的操作序列，最多花费 \(O(n)\)时间。一个操作的平均时间为\(O(n)/n=O(l)\)。在聚合分析中，我们将每个操作的摊还代价设定为平均代价。因此，在此例中，所有三种栈操作的摊还代价都是\(O(1)\)。

核算法

为了说明摊还分析的核算法，我们回到栈的例子。回顾前面的内容，操作的实际代价为:

PUSH : 1
POP : 1
MULTIPOP : \(\min(k,s)\) (其中\(k\)是提供给MULTIPOP的参数，\(s\)是调用时栈的规模)
PUSH : 2
POP : 0
MULTIPOP : 0
MULTIPOP的摊还代价是一个常数 (0),而其实际代价是变量。在此例中，所有三个摊还代价都是常数。一般来说，所考虑的操作的摊还代价可能各不相同，渐近性也可能不同。
在PUSH每个盘子的时候，就为其POP存下一美元信用。
换句话说，由千栈中的每个盘子都存有 1美元的信用，而栈中的盘子数始终是非负的，因此可以保证信用值也总是非负的。因此，对任意 \(n\)个 PUSH、 POP、MULTIPOP操作组成的序列，总摊还代价为总实际代价的上界。由千总摊还代价为 \(O(n)\),因此总实际代价也是。

势能法

我们将一个栈的势函数定义为其中的对象数量。对于初始的空栈\(D_0\),我们有 \(\Phi(D_0) =0\)。由千栈中对象数目永远不可能为负，因此，第\(i\)步操作得到的栈 \(D_i\);具有非负的势
POP的摊还代价： 0
PUSH的摊还代价：2

二进制计数器递增¶

例子描述

我们来看一个\(K\)位二进制计数器递增的问题，计数器的初值为\(0\)。我们用一个位数组 \(A[0.. k—1]\)作为计数器，其中 \(A.length=k\)。当计数器中保存的二进制值为\(x\)时，\(x\)的最低位保存在 \(A[0]\)中，而最高位保存在 \(A[k-1]\)中，因此\(x= \sum\limits_{i=0}^{k-1}{A[i]}•2^i\)。初始时 \(x=0\),因此对所有 \(i=0, 1, …, k-1, A[i]=0\)。为了将 \(1\)(模 \(2^k\))加到计数器的值上，我们使用如下过程：

INCREMENT(A)
    i = 0
    while i < A.lenght and A[i] ==1 :
        A[i] = 0
        i = i + 1
    if i < A.lenght:
        A[i] = 1

与上一个关于栈的例子类似，对此算法的运行时间进行粗略的分析会得到一个正确但不紧的界。最坏情况下 INCREMENT执行一次花费\(O(k)\)时间，最坏情况当数组A所有位都为 1时发生。因此，对初值为 0的计数器执行 \(n\)个INCREMENT操作最坏情况下花费 \(O(nk)\)时间。

聚合分析

对于\(n\)个 INCREMENT操作组成的序列，我们可以得到一个更紧的界（最坏情况下代价）为 \(O(n)\),因为不可能每次 INCREMENT操作都翻转所有的二进制位。每次调用INCREMENT时 \(A[0]\)确实都会翻转。而下一位 \(A[1]\),则只是每两次调用翻转一次，这样，对一个初值为 \(0\)的计数器执行一个\(n\)个INCREMENT操作的序列，只会使\(A[1]\)翻转 \([n/2]\)次。类似地， \(A[2]\)每4次调用才翻转一次，即执行一个\(n\)个INCREMENT操作的序列的过程中翻转\([n/4]\)次。一般地，对一个初值为\(0\)的计数器，在执行一个由\(n\)个INCREMENT操作组成的序列的过程中，\(A[i]\)会翻转\([n/2^i]\)次 \((i=0, 1, …， K-1)\)。对 \(i ≥ k\), \(A[i]\)不存在，因此也就不会翻转。因此，在执行 INCREMENT序列的过程中进行的翻转操作的总数为

\[\sum\limits_{i=0}^{k-1}{[\frac{n}{2^i}]} < n\sum\limits_{i=1}^{\infty}{\frac{1}{2^i}} = 2n\]

因此，对一个初值为\(0\)的计数器，执行一个\(n\)个 INCREMENT操作的序列的最坏情况时间为\(O(n)\)。每个操作的平均代价，即摊还代价为\(O(n)/n=O(1)\)。

核算法

我们分析在一个从\(0\)开始的二进制计数器上执行 INCREMENT操作。如我们之前所观察到的，此操作的运行时间与翻转的位数成正比，因此对此例，可以将翻转的位数作为操作的代价。我们再次使用\(1\)美元表示一个单位的代价（在此例中是翻转\(1\)位）。在摊还分析中，对一次置位操作，我们设其摊还代价为\(2\)美元。当进行置位时，用\(1\)美元支付置位操作的实际代价，并将另外\(1\)美元存为信用，用来支付将来复位操作的代价。在任何时刻，计数器中任何为\(1\)的位都存有\(1\)美元的信用，这样对千复位操作，我们就无需缴纳任何费用，使用存储的 1美元信用即可支付复位操作的代价。现在可以确定 INCREMENT的摊还代价。 while循环中复位操作的代价用该位储存的\(1\)美元来支付。INCREMENT过程至多置位一次，因此，其摊还代价最多为\(2\)美元。计数器中\(1\)的个数永远不会为负，因此，任何时刻信用值都是非负的。所以，对于\(n\)个INCREMENT操作，总摊还代价为\(O(n)\),为总实际代价的上界。

势能法

作为势能法的另一个例子，我们再次分析二进制计数器递增问题。这一次，我们将计数器执行\(i\)次 INCREMENT操作后的势定义为\(b_i\)(\(i\)次操作后计数器中1的个数)。我们来计算 INCREMENT操作的摊还代价。假设第\(i\)个INCREMENT操作将\(t_i\)个位复位，则其实际代价至多为\(t_i + 1\),因为除了复位\(t_i\)个位之外，还至多置位1位。如果 \(b_i=0\),则第\(i\)个操作将所有\(K\)位都复位了，因此 \(b_{i-1} =t_i=k\)。如果 \(b_i>0\),则 \(b_i=b_{i-1}-t_i+1\)。无论哪种情况，\(b_i \leq b_{i-1}-1-t_i + 1\),势差为

\[\Phi(D_i) - \Phi(D_{i-1}) \leq (b_{i-1} - t_i + 1) - b_{i-1} = 1 - t_i\]

因此，摊还代价为

\[\hat{c_i} = c_i + \Phi(D_i) - \Phi(D_{i-1}) \leq (t_1 + 1) + (1 - t_i) = 2\]

如果计数器从\(0\)开始，则\(\Phi(D_0) = 0\)由于对所有i均有\(\Phi(D_i) \geq 0\), 因此，一个\(n\)个INCREMENT操作的序列的总摊还代价是总实际代价的上界，所以 n个INCREMENT操作的最坏情况时间为\(O(n)\)。势能法给出了分析计数器问题的一个简单方法，即使计数器不是从\(0\)开始也可以分析。计数器初始时包含\(b_0\)个1,经过n个INCREMENT操作后包含\(b_n\)个1,其中\(0 \leq b_0, b_n \leq k\)

\[\sum\limits_{i=1}^{n}c_i = \sum\limits_{i=1}^{n}\hat{c_i} + \Phi(D_0) - \Phi(D_n)\]

\[\sum\limits_{i=1}^{n}c_i \leq \sum\limits_{i=1}^{n}2-b_n+b_0=2n-b_n+b_0\]