跳转至

chapter 4 Leftist Heap & Skew Heap

本讲的难点在于理解对应的摊还分析

Review of heap
  1. Insert：我们直接插在完全二叉树的下一个空位上，然后 percolate up 找到它应当在的位置，显然最坏情况也与完全二叉树的高度成正比，即 \(O(\log n)\)。
  2. FindMin：直接返回根结点即可，时间 \(O(1)\)。
  3. DeleteMin：直接用完全二叉树的最后一个元素顶替根结点，然后 percolate down 找到新根结点的归宿，时间 \(O(\log n)\)
  4. Buildheap : 一般从最后的父节点开始维护
  5. merge:把一个接到另一个后面，完了按照build的过程处理

Leftist Heaps

definition

  • Target : Speed up merging in \(O(N)\).
  • Heap:Structure Property + Order Property
  • The null path length, \(Npl(X)\)(到外结点的路径长度), of any node X is the length of the shortest path from \(X\) to a node without two children. Define \(Npl(NULL) = –1\).
  • The leftist heap property is that for every node \(X\) in the heap, the null path length of the left child is at least as large as that of the right child.

NPL

\(\textbf{Npl}(X)\) = \(\min\) { \(\textbf{Npl}(C) + 1 \quad \text{for all C as children of X}\) }

  • Order Property – the same
  • Structure Property – binary tree, but unbalanced

性质:

  • A leftist tree with \(r\) nodes on the right path must have at least \(2^r – 1\) nodes(左倾堆的NPL等于右路径)
  • 右路径长度的渐进上界是\(O(\log N)\)
  • 判断以下两个说法是否正确，若正确，请给出详细的证明；若不正确，请举出反例：
    1. 按顺序将含有键值\(1, 2, · · · , 2^k − 1\)的结点从小到大依次插入左式堆，那么结果将形成一棵完全平衡的二叉树。
    2. 按顺序将含有键值\(1, 2, · · · , 2^k − 1\)的结点从小到大依次插入斜堆，那么结果将形成一棵完全平衡的二叉树。两个结果都是正确的，证明只需要找规律归纳即可，没有什么特殊性。除此之外，斜堆的 Delete和 DecreaseKey 操作我们一般不讨论。

Declaration

struct TreeNode 
{ 
    ElementType     Element;
    PriorityQueue       Left;
    PriorityQueue       Right;
    int         Npl;
};

Merge

递归实现

  1. 如果两个堆中至少有一个是空的，那么直接返回另一个即可；
  2. 如果两个堆都非空，我们比较两个堆的根结点 key 的大小，key 小的是 \(H_1\)，key 大的是 \(H_2\)；
  3. 如果 \(H_1\) 只有一个顶点（根据左式堆的定义，只要它没有左孩子就一定是单点），直接把 \(H_2\) 放在 \(H_1\) 的左子树就完成任务了（很容易验证这样得到的结构符合左式堆性质，此时 \(Npl\) 也没有变化）；
  4. 如果 \(H_1\) 不只有一个顶点，则将 \(H1\) 的右子树和 \(H_2\) 合并（这是递归的体现，在 base case 设计良好，其它步骤也都合理的情况下你完全可以相信这一步递归帮你做对了），成为 \(H_1\) 的新右子树；
  5. 如果 \(H_1\) 的 \(Npl\) 性质被违反，则交换它的两个子树；
  6. 更新 \(H_1\) 的 \(Npl\)，结束任务。

复杂度分析

  • 在将递归过程展开之后，我们就可以很清楚地分析时间复杂度。我们首先分析递归的最大深度。我们发现，在\(1-5\)步这样的递归过程中，产生的递归层数不会超过两个左式堆的右路径长度之和，因为每次递归都会使得两个堆的其中一个（根结点key更小的）向着右路径上下一个右孩子推进，并且直到其中一个推到了null结点就不再加深递归。注意加深一层的过程中的操作是常数的，因为只需要简单的大小比较和找孩子，加上右路径长度的限制，因此递归向下的过程是\(O(\log n)\)的。这一点我们可以更严谨地展开：假设\(H_1\)大小为\(N_1\)，\(H_2\)大小为\(N_2\)，两者路径之和\(\(O(\log N_1 + \log N_2) = O(\log N_1N_2) = O(\log \sqrt{N_1N_2}) = O(\log(N1 + N2))\)\),上面的推导用到了基本不等式 \(a + b ⩾ 2\sqrt{ab}\)。总而言之，两个堆右路径长度之和仍然是两个堆大小的对数级别，因此递归层数是\(O(\log n)\)的是准确的。接下来分析递归返回的操作，事实上每一层的操作也是常数的，因为只需要接上新的指针，判断、交换子树以及更新 Npl，所以也是\(O(\log n)\)的，因此总的时间复杂度就是 \(O(\log n)\)的。

迭代实现

迭代事实上就是两个指针指向未被Merge的子树的根节点，做一个归并排序

Skew Heaps

Definition

  • Target : Any M consecutive operations take at most \(O(M \log N)\) time
  • Always swap the left and right children except that the largest of all the nodes on the right paths does not have its children swapped. No Npl.

Example

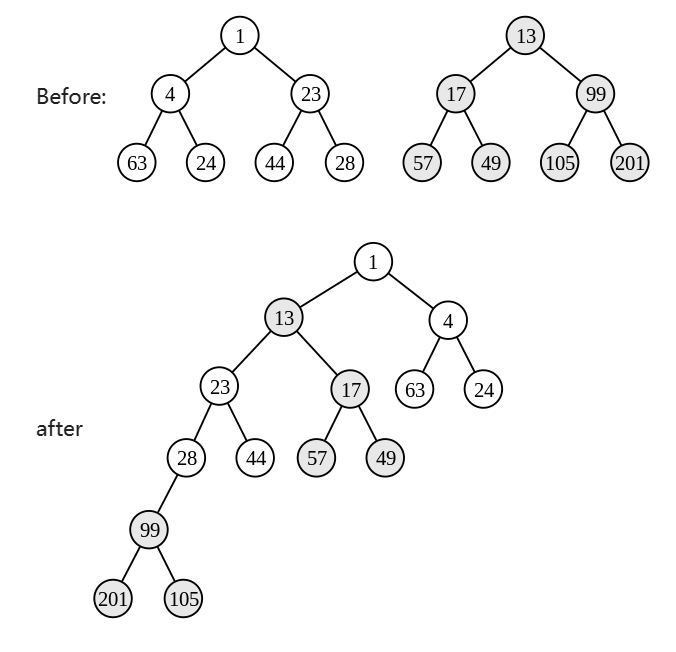- 详细过程

Difference between skew heap and leftist heap

  • 在base case是处理\(H\)与null连接的情况时，左式堆直接返回\(H\)即可，但斜堆必须看\(H\)的右路径，我们要求\(H\)右路径上除了最大结点之外都必须交换其左右孩子。
  • 在非base case时，若\(H_1\)的根结点小于\(H_2\)，如果是左式堆，我们需要合并\(H_1\)的右子树和 H2作为\(H_1\)的新右子树，最后再判断这样是否违反性质决定是否交换左右孩子，斜堆直接无脑交换，也就是说每次这种情况都把\(H_1\)的左孩子换到右孩子的位置，然后把新合并的插入在\(H_1\)的左子树上。

Note

  • Skew heaps have the advantage that no extra space is required to maintain path lengths and no tests are required to determine when to swap children.
  • It is an open problem to determine precisely the expected right path length of both leftist and skew heaps.

摊还分析

  • 我们称一个结点 \(P\) 是重的（heavy），如果它的右子树结点个数至少是 \(P\) 的所有后代的一半 （后代包括 \(P\) 自身）。反之称为轻结点（light node）
  • 对于右路径上右 \(l\) 个轻结点的斜堆，整个斜堆至少有 \(2^l − 1\) 个结点，这意味着一个 \(n\) 个结点的斜堆右路径上的轻结点个数为 \(O(\log n)\)
  • 若我们有两个斜堆 \(H_1\) 和 \(H_2\)，它们分别有 \(n_1\) 和 \(n_2\) 个结点，则合并 \(H_1\) 和 \(H_2\) 的摊还时间复杂度为\(O(\log n)\)，其中 \(n = n1 + n2\)
Proof
  • 我们定义势函数 \(Φ(H_i)\) 等于堆 \(H_i\) 的重结点（heavy node）的个数，并令 \(H_3\) 为合并后的新堆.我们设 \(H_i(i = 1, 2)\) 的右路径上的轻结点数量为 \(l_i\)，重结点数量为 \(h_i\)，因此真实的合并操作最坏的时间复杂度为 \(c_i = l_1 + l_2 + h_1 + h_2\)（所有操作都在右路径上完成）。因此根据摊还分析我们知道摊还时间复杂度为\(\hat{c_i} = c_i + Φ(H3) − (Φ(H1) + Φ(H2))\)事实上，在 merge 前我们可以记\(Φ(H_1) + Φ(H_2) = h_1 + h_2 + h\)其中 \(h\) 表示不在右路径上的重结点个数。现在我们要考察合并后的情况，事实上我们有两个非常重要的观察：
  1. 只有在 \(H_1\) 和 \(H_2\) 右路径上的结点才可能改变轻重状态，这是很显然的，因为其它结点合并前后子树是完全被复制的，所以不可能改变轻重状态；
  2. \(H_1\)和\(H_2\)右路径上的重结点在合并后一定会变成轻结点，这是因为右路径上结点一定会交换左右子树，并且后续所有结点也都会继续插入在左子树上（这也表明轻结点不一定变为重结点）。结合以上两点，我们知道合并后原本不在右路径上的\(h\)个重结点仍然是重结点，在右路径上的\(h_1 + h_2\)个重结点全部变成轻结点，\(l_1 + l_2\) 个轻结点不一定都变重，因此合并后我们有\(Φ(H_3) ⩽ l_1 + l_2 + h\),代入数据计算可得\(c_i ⩽ (l_1 + l_2 + h_1 + h_2) + (l_1 + l_2 + h) − (h_1 + h_2 + h) = 2(l_1 + l_2)\).根据前面的引理，\(l_1 + l_2 = O(\log n_1 + \log n_2) = O(\log(n_1 + n_2)) = O(\log n)\)（这里的等号之前有完全一样的说明过），并且注意到初始（空堆）势函数一定为 \(0\)。且之后总是非负的，所以这一势函数定义满足要求，因此我们的证明也就完成了。

怎么感觉yy上课讲复杂了

评论