chapter 2 Arithmetic for Computer¶

Quote

本周计组是对着HobbitQia的笔记本和马德老师的智云自己补的XD

Abstract

Introduction
Signed and Unsigned Numbers-Possible Representations
Arithmetic--Addition & subtraction and ALU
Multiplication
Division
Floating point numbers

Warning

本周计组涉及到了计逻中的ALU，CLA等概念

Introduction¶

Instructions can be divided into 3 categories

memory-reference instructions
e.g. lw, sw 需要 ALU 计算内存地址
arithmetic-logical instructions
e.g. add, sub, and, or, xor, slt 需要 ALU 进行计算
control flow instructions
e.g. beq, bne, jal 需要 ALU 进行条件判断

Signed Number Formats¶

Sign and magnitude
2's Complement
1's Complement
Biased notation

Why we need biased notation

上图是 32 位的二进制补码表示，我们可以看到左侧二进制表示，如果看作无符号数，那他们是从小到大排列的；但右侧对应的十进制整数确实分段单增的。
我们希望有一种这样的表示，能够让右侧的对应的值也单调递增。
一个想法是对右侧数加上 $2^{31}$, 相当于其二进制表示下最高位翻转。

$[X]_b = 2^n + X$ 从二进制补码到移码，只需要翻转符号位即可。

Overflow¶

出现Overflow时候，记录当前指令地址，然后跳转专门处理异常指令的地方

The sum of two numbers can exceed any representation
The difference of two numbers can exceed any representation
2's complement:Numbers change sign and size

Example

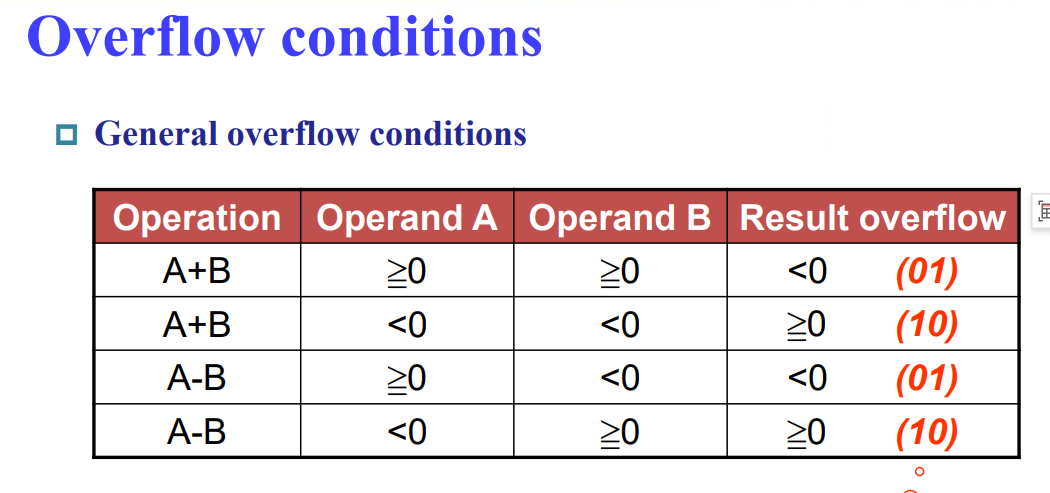
Reaction of Overflow¶

An exception (interrupt) occurs
- Control jumps to predefined address for exception
- Interrupted address is saved for possible resumption
Signaling to application (Ada, Fortran)
Ignore, don't always want to detect overflow
note: sltu, sltiu for unsigned comparisons

Overflow process¶

Hardware detection in the ALU
- Generation of an exception (interrupt)
Save the instruction address (not PC) in special register SEPC
Jump to specific routine in OS
- Correct & return to program
- Return to program with error code
- Abort program

Logical Operation¶

Logical operations¶

Logical shift operation
right (srl)
left (sll)

The machine instruction for the instruction¶

slli x11, x9, 3

Constructing an ALU¶

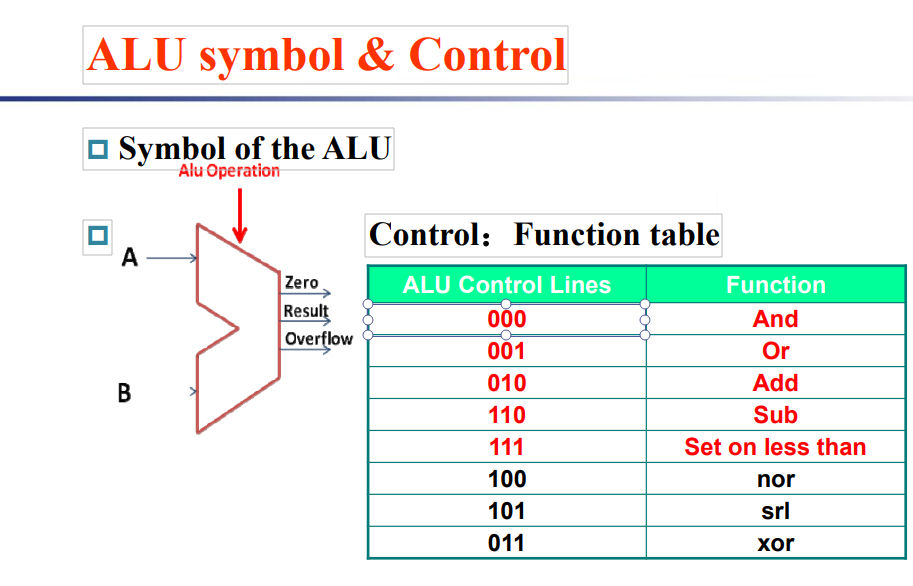
ALU symbol & Control¶

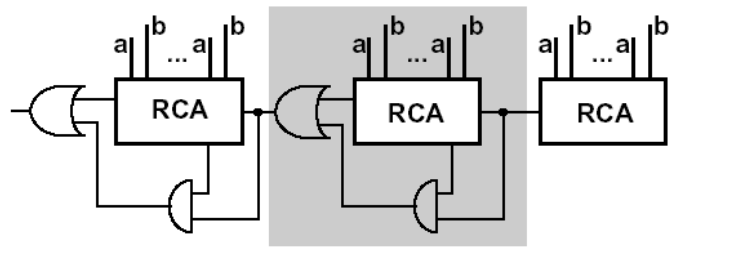
Carry skip adder(跳跃加法器)¶

Accelerating the carry by skipping the interior blocks
Optimal speed with no-equal distribution of block length

Arithmetic¶

Substraction
Overflow detection: $C_n \oplus C_{n-1}$

注: RISC-V 不支持 nor 指令。

Multiplication¶

Unsigned multiplication¶

Multiplicand (被乘数) $\times$ Multiplier (乘数)

如果乘数末位是 1, 加被乘数，否则加 0. 随后将被乘数左移 1 位。

需要 128+128+64 bit 的寄存器，和一个 128 bit ALU.
不移被乘数，而是移积 (product). 这样 ALU 只需要 64 位。

Example
这里积最开始只保存在左半部分，右半部分为空。而乘数也要右移，这样我们可以把两个数拼到一起，同时右移。

Signed multiplication¶

有符号相乘不能直接乘，可以先用符号位决定结果符号，再对绝对值进行乘法。

Booth's Algorithm

思想：如果有一串$1$ - 减掉乘数的第一个1 - 后面的1的序列进行移位 - 当上一步是最后一个1时加
最开始把积放在高位，被乘数放在低位。（数据保存方法同 2.1.1）默认 $bit_{-1}=0$

Action
- 10 - subtract multiplicand from left
- 11 - nop
- 01 - add multiplicand to left half
- 00 - nop
每个操作结束后都要移位，和 2.1.1 中类似

注意移位时不要改变符号位。

Example

被乘数 Multiplicand 是 0010, 乘数 Multiplier 是 1101.
最开始将积 0000 放在高四位, 1101 作为乘数放在低四位。最开始 10, 即执行减操作, $0000-0010=1110$. 答案依然放在高四位，随后右移，以此类推。
注意右移的时候是算术右移, $bit_{-1}$ 也可能会改变。

Faster Multiplication¶

32 位数乘 32 位数，相当于 32 个 32 位数相加。（并行加速）

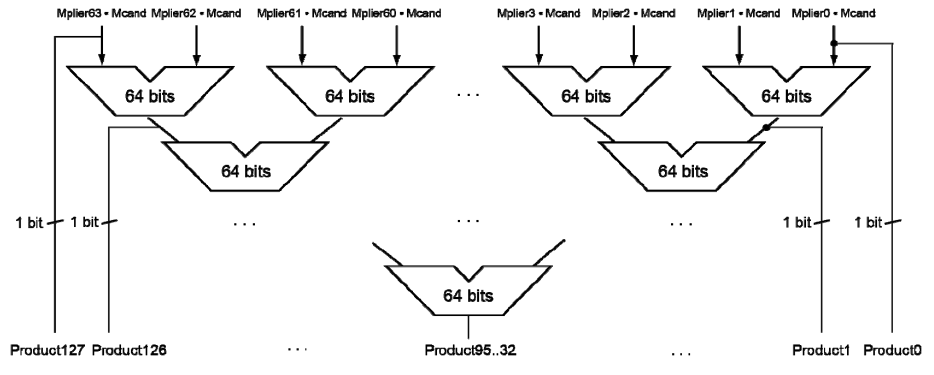
Division¶

Dividend (被除数) $\div$ Divisor (除数)

将除数放到高位。从高位开始减，减完将除数右移。商也随之不断左移。如果减完之后是负数，需要还回去。

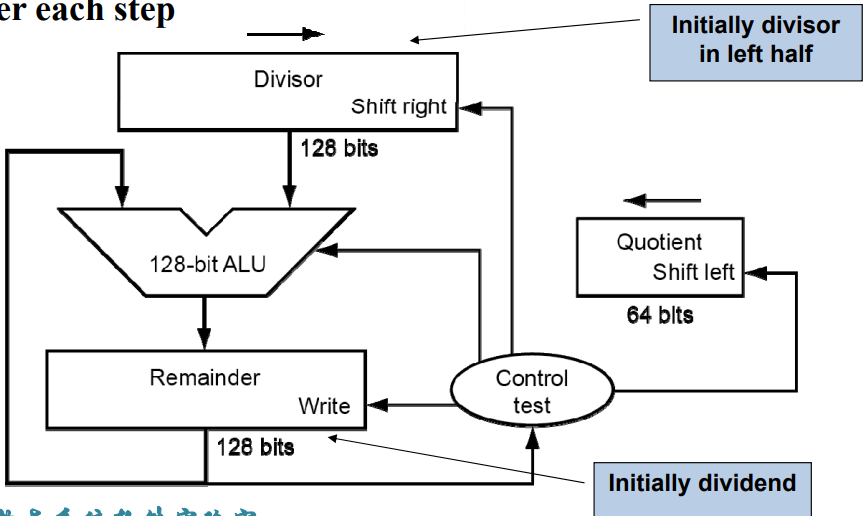
7÷2

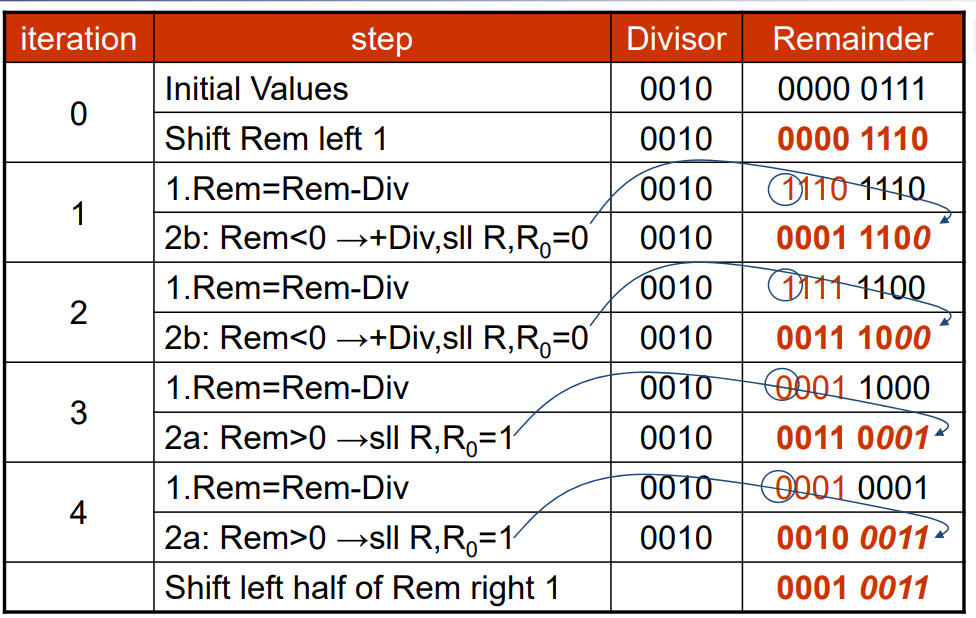
除数不动，被除数不停地往左移。减到最后一次，如果是小于 0 的，说明不用减了，剩下的就是余数，需要右移移回来。（即将左半部分右移一位)因为每次都是将除数和被除数最高位减，减了之后高位就没用了，可以移出去。

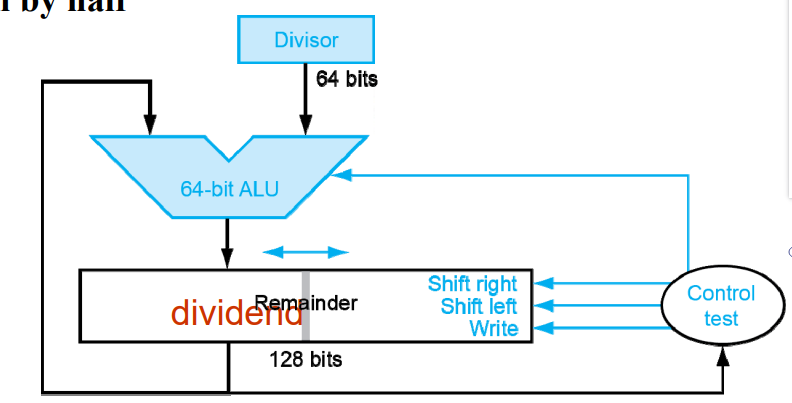
实际上这里结果是 129 位，防止 carry 丢失

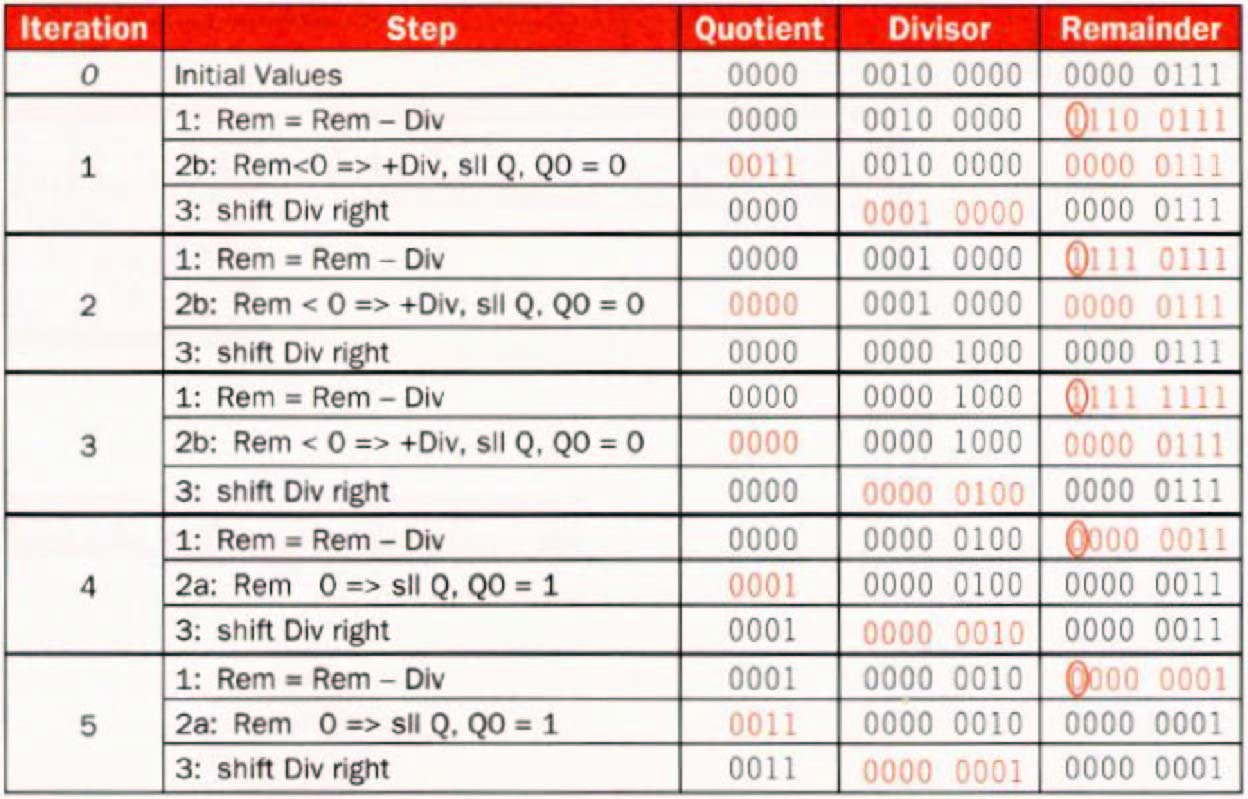
Example

这里最开始余数就是整个被除数。
类似乘法，这里的除数只和被除数的高位相减。如果减出来是负数，需要加回去。每次减完之后先左移，然后最右边的一位放商。4.1 时其实我们已经结束了除法操作，此时的高位就是我们的余数，但是这最后一次的结果还没有放回到 Reminder 中，因此我们需要再往左移一位为商留出空间，放入后，再把高位余数往右移动以抵消影响。

signed division¶

带符号的除法：要求余数和被除数符号相同。
除零会产生溢出，由软件检测。

RISC-V Division¶

Four instructions:
- div, rem: signed divide, remainder
- divu, remu: unsigned divide, remainder
Overflow and division-by-zero don’t produce errors
- Just return defined results
- Faster for the common case of no error

Float¶

Reasoning
- Larger number range than integer rage
- Fractions
- Numbers like e (2.71828) and π(3.14159265....)
Representation for non-integral numbers
- Including very small and very large numbers
Like scientific notation
- $–2.34 × 10^{56}$规范的科学计数法
- $+0.002 × 10^{–4}$首位为0
- $+987.02 × 10^{9}$

IEEE Floating-Point Format¶

S: sign bit (0 $\rightarrow$ non-negative, 1 $\rightarrow$ negative)
Normalize significand: $1.0 ≤ |\textbf{significand}| < 2.0$
- Always has a leading pre-binary-point 1 bit, so no need to represent it explicitly (hidden bit)
- Significand is Fraction with the “1.” restored
Exponent: excess representation: actual exponent + Bias
- Ensures exponent is unsigned
- 偏移量：Single: Bias = 127; Double: Bias = 1023

Range¶

单精度范围

双精度范围

Relative precision
- all fraction bits are significant
- Single: approx $2^{–23}$
  - Equivalent to $23 × \log_{10}2 ≈ 23 × 0.3 ≈ 7 $decimal digits of precision
- Double: approx 2–52
  - Equivalent to $52 × \log_{10}2 ≈ 52 × 0.3 ≈ 16 $decimal digits of precision

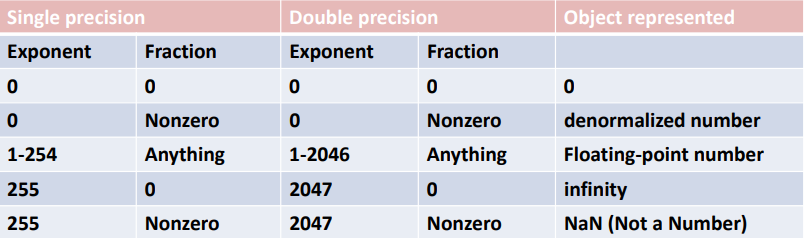
Denormal Numbers¶

$Exponent=000\ldots 0$
非规格化数，让数在较小时能逐渐下溢出。
$x=(-1)^s\times((0+Fraction)\times 2^{1-Bias})$
注意此时指数是 $1-Bias=-126/-1022$.
- Denormal with $Fraction = 000...0$ we define $x=0$
$Exponent=111\ldots 1, Fraction=000\ldots 0$
表示 $\pm \inf$
$Exponent=111\ldots 1, Fraction\neq 000\ldots 0$ 表示 NaN (Not-a-Number)

addition¶

将指数更小的浮点数的有效部分右移对齐(Truncation)

Example

FP Adder Hardware¶

蓝色线为控制通路，黑色线为数据通路

Much more complex than integer adder
Doing it in one clock cycle would take too long
- Much longer than integer operations
- Slower clock would penalize all instructions
FP adder usually takes several cycles
- Can be pipelined

Floating-Point Multiplication¶

$(s1\cdot 2^{e1}) \cdot (s2\cdot 2^{s2}) = (s1\cdot s2)\cdot 2^{e1+e2}$

Add exponents
Multiply the significands
Normalize
Over/Underflow?
有的话要抛出异常，通过结果的指数判断。
Rounding
Sign

注意 Exponet 中是有 Bias 的，两个数的 exp 部分相加后还要再减去 Bias.

Example

Data Flow

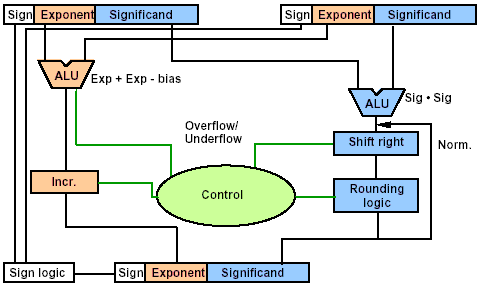
右边往回的箭头: Rounding 后可能会进位。
Incr 用于标准化结果，与右侧 Shift Right 配合。

Parallelism and Computer Arithmetic: Associativity¶

浮点数运算受运算顺序影响

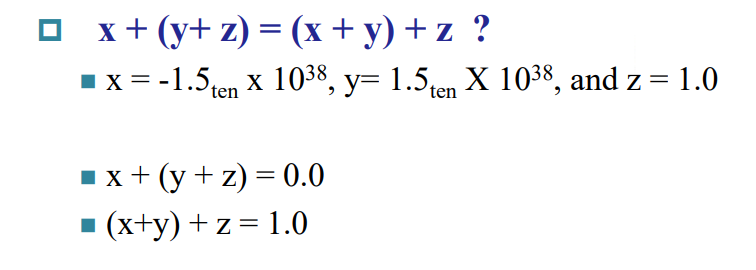
FP Instructions in RISC-V¶

Separate FP registers: f0, …, f31
- double-precision
- single-precision values stored in the lower 32 bits
FP instructions operate only on FP registers
- Programs generally don’t do integer ops on FP data, or vice versa
- More registers with minimal code-size impact
FP load and store instructions
- flw, fld
- fsw, fsd
Single-precision arithmetic
- fadd.s, fsub.s, fmul.s, fdiv.s, fsqrt.s
  - e.g., fadds.s f2, f4, f6
Double-precision arithmetic
- fadd.d, fsub.d, fmul.d, fdiv.d, fsqrt.d
  - e.g., fadd.d f2, f4, f6
Single- and double-precision comparison
- feq.s, flt.s, fle.s
- feq.d, flt.d, fle.d
- Result is 0 or 1 in integer destination register
  - Use beq, bne to branch on comparison result
Branch on FP condition code true or false
- B.cond

chapter 2 Arithmetic for Computer¶

Introduction¶

Signed Number Formats¶

Overflow¶

Reaction of Overflow¶

Overflow process¶

Logical Operation¶

Logical operations¶

The machine instruction for the instruction¶

Constructing an ALU¶

ALU symbol & Control¶

Carry skip adder(跳跃加法器)¶

Arithmetic¶

Multiplication¶

Unsigned multiplication¶

Signed multiplication¶

Faster Multiplication¶

Division¶

signed division¶

RISC-V Division¶

Float¶

IEEE Floating-Point Format¶

Range¶

Denormal Numbers¶

addition¶

FP Adder Hardware¶

Floating-Point Multiplication¶

Parallelism and Computer Arithmetic: Associativity¶

FP Instructions in RISC-V¶

评论