Denoising Diffusion Probabilistic Models¶
Reference¶
去噪扩散概率模型(Denoising Diffusion Probabilistic Models)
Definition¶
Diffusion Model有两个过程:前向过程(forward process)和反向过程(reverse process),其中前向过程又称为扩散过程(diffusion process)。无论是前向过程还是反向过程都是一个参数化的马尔可夫链(Markov chain),其中反向过程可用于生成数据样本(它的作用类似GAN中的生成器,只不过GAN生成器会有维度变化,而DDPM的反向过程没有维度变化)。
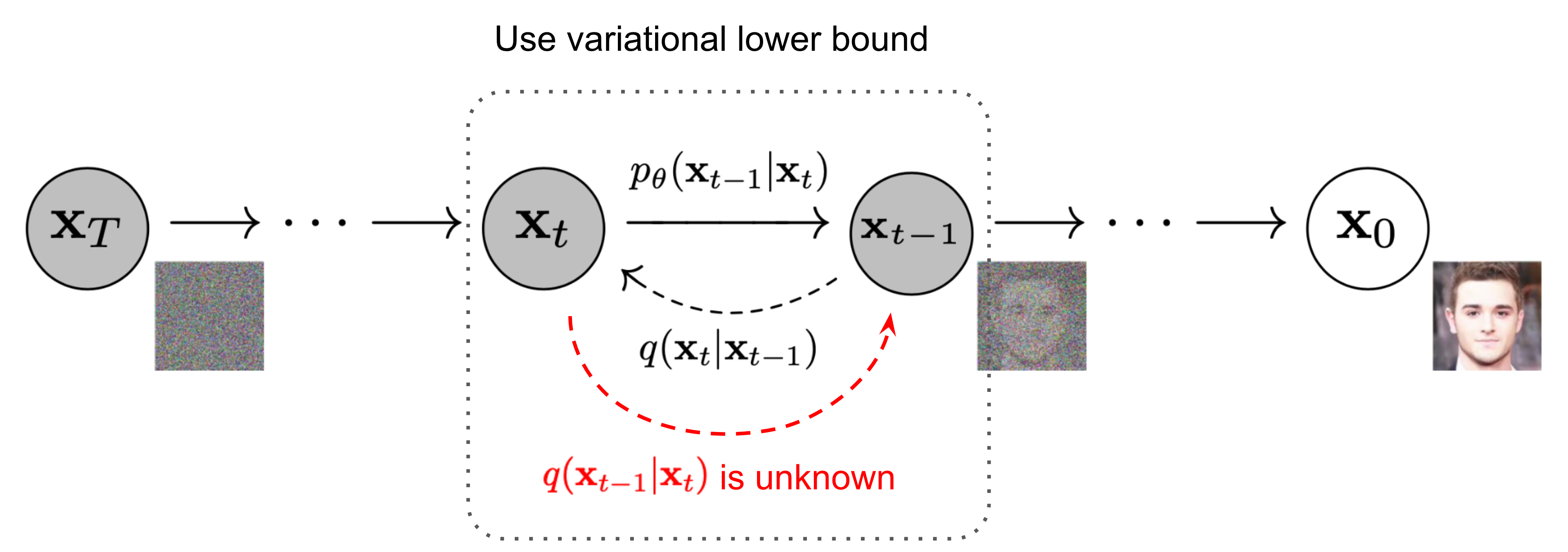
- \(X_0\) 到\(X_t\)为逐步加噪过的前向程,噪声是已知的,该过程从原始图片逐步加噪至一组纯噪声。
- \(X_t\)到\(X_0\)为将一组随机噪声还原为输入的过程。该过程需要学习一个去噪过程,直到还原一张图片。
Forward Process¶
前向过程是加噪的过程,前向过程中图像\(\mathbf{x}_t\)只和上一时刻的\(\mathbf{x}_{t-1}\)有关, 该过程可以视为马尔科夫过程, 满足:
\[
q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) \quad q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1})
\]
可以推出\(\mathbf{x}_0\)与\(\mathbf{x}_{t}\)的关系如下
\[
\begin{aligned}
\mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1} & \text{ ;where } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\boldsymbol{\epsilon}}_{t-2} & \text{ ;where } \bar{\boldsymbol{\epsilon}}_{t-2} \text{ merges two Gaussians (*).} \\ & = \dots \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon} \\ q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I})
\end{aligned}
\]
\[
\alpha_t = 1 - \beta_t \quad \bar{\alpha}_t = \prod_{i=1}^t \alpha_i
\]
注:\(\beta_t\)由对应时刻\(t\)决定,
这个过程中,随着\(t\)的增大, \(\mathbf{x}_t\)越来越接近纯噪声。当\(t\)→∞ , \(\mathbf{x}_t\)是完全的高斯噪声
reverse process¶
\[
p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T) \prod^T_{t=1} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \quad p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))
\]
Characteristic¶
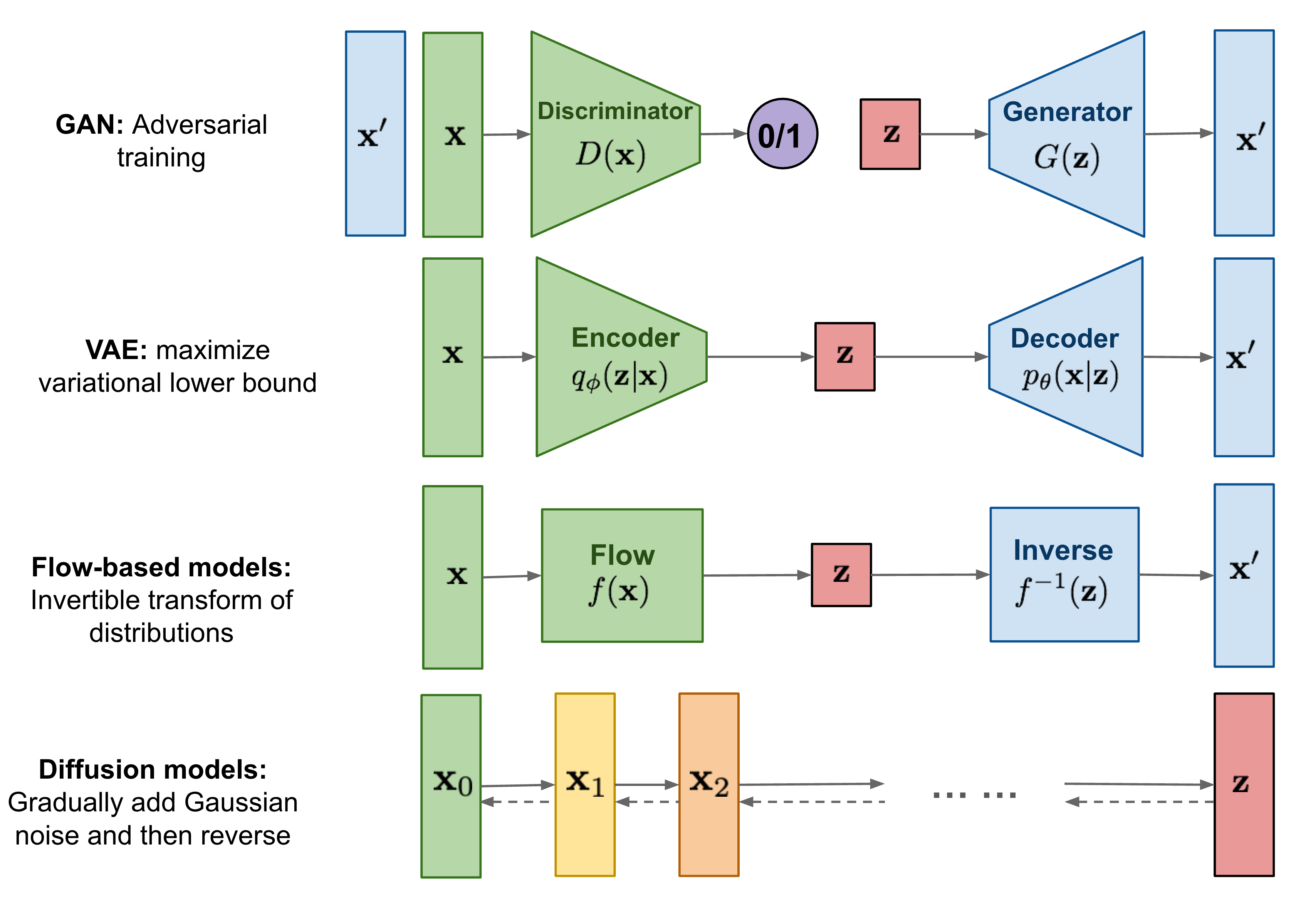
diffusion model和其他模型最大的区别是它的latent code(z)和原图是同尺寸大小的
重参数(reparameterization trick)¶
\[
\mathbf{x}_t = \mathbf{x}_{t-1} + \frac{\delta}{2} \nabla_\mathbf{x} \log p(\mathbf{x}_{t-1}) + \sqrt{\delta} \boldsymbol{\epsilon}_t
,\quad\text{where }
\boldsymbol{\epsilon}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I})
\]